Пространство выборки, события и вероятности
Множество
Начнем с определения множества. Множество — это коллекция объектов, которые могут быть чем угодно: числа, люди, автомобили и т.д.
Множество бывает конечным или бесконечным. Например, множество всех натуральных чисел (от 1 до бесконечности) — бесконечно, а множество всех людей на Земле — конечно.
Математически множество обозначается фигурными скобками. Например, множество всех натуральных чисел от 1 до 10:
$$ \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} $$Множество может быть пустым: \(\emptyset\) или \(\{\}\). Пустое множество не содержит ни одного элемента.
Пример:
Множество всех натуральных чисел:
$$ \mathbb{N} = \{1, 2, 3, 4, 5, \ldots\} $$Множество всех целых чисел:
$$ \mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\} $$Множество всех действительных чисел:
$$ \mathbb{R} = \{x \mid x \text{ — действительное число}\} $$Подмножество
Если множество B является частью множества A, то B — подмножество A.
Например, если \(A = \{1,2,3\}\), то возможные подмножества: \(\emptyset\), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,2\}\), \(\{1,3\}\), \(\{2,3\}\), \(\{1,2,3\}\).
Обозначается как \(B \subseteq A\). Если B не является подмножеством A, пишут \(B \nsubseteq A\).
Пространство выборки (Sample Space)
Пространство выборки — это множество всех возможных исходов эксперимента.
Например, при броске кубика пространство выборки:
$$ S = \{1, 2, 3, 4, 5, 6\} $$При броске монеты:
$$ S = \{\text{орел}, \text{решка}\} $$Если бросаем кубик дважды:
$$ S = \{ (1,1), (1,2), \ldots, (6,5), (6,6) \} $$Пространство выборки всегда зависит от конкретного эксперимента, который мы проводим.
Пример пространства выборки для броска кубика:
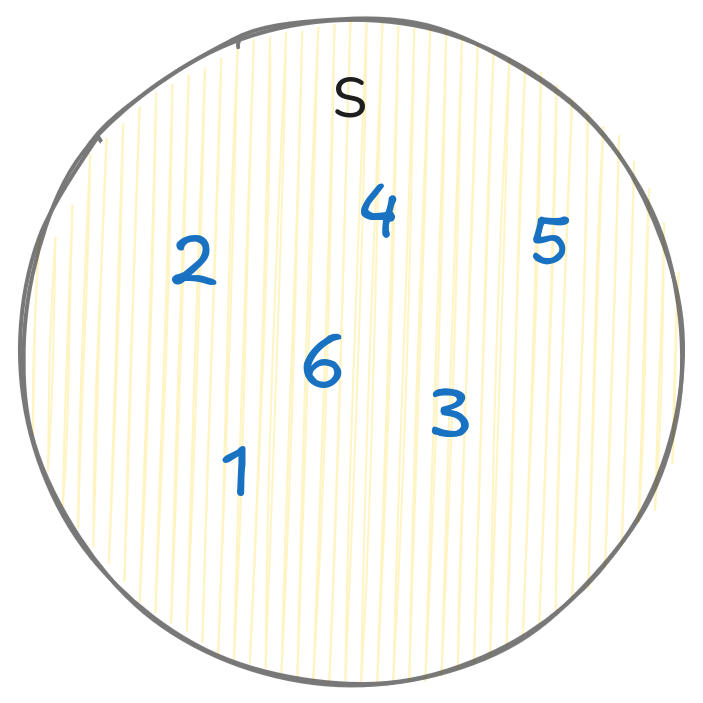
Событие
Любое подмножество пространства выборки называется событием (обозначим его как E).
Например, при броске кубика событие “выпало четное число”:
$$ E = \{2, 4, 6\} $$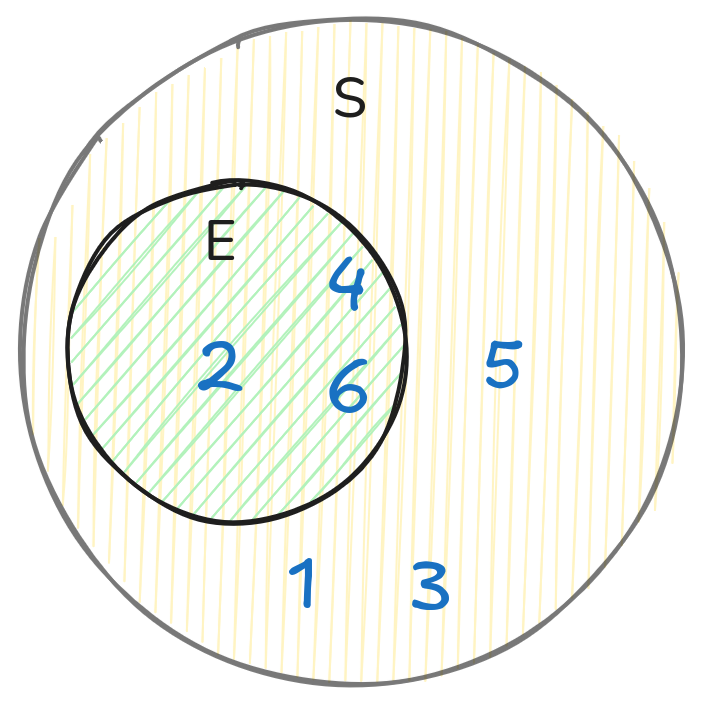
Запомним: событие \(E\) — подмножество пространства выборки \(S\), то есть \(E \subseteq S\).
E может быть пустым (например, событие “выпало число больше 6” при броске кубика).
Вероятность
Вероятность — мера того, насколько вероятно, что событие произойдет. Вероятность события E обозначается \(P(E)\).
Интуитивно, вероятность события E — это отношение числа благоприятных исходов к общему числу исходов в пространстве выборки (то есть количества элементов в E к количеству элементов в S):
$$ P(E) = \frac{|E|}{|S|} \tag{1} $$где \(|E|\) — количество элементов в E.
Пример:
Для примера с кубиком вероятность выпадения четного числа:
$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Так как \(|E| \leq |S|\), вероятность события E всегда лежит в пределах от 0 до 1.
- При вероятности 0 событие никогда не произойдет.
- При вероятности 1 событие произойдет всегда.
Важно: Рассчитывать вероятность таким подсчетом благоприятных исходов можно только если все исходы равновероятны. Этот подход называется классическим.
Но если, например, наш кубик неравновероятный (со смещённым центром тяжести), то вероятность выпадения 1, например, будет уже не 1/6.
Если хотя бы один из исходов предпочтительнее, такой метод перестаёт отражать реальную вероятность, и нужно использовать фактические частоты. Так, если мы бросаем кубик 100 раз и 20 раз выпадает 1, то вероятность выпадения 1 будет 20/100 = 0.2.
В такой ситуации вероятность КАЖДОГО ОТДЕЛЬНОГО события можно посчитать частотным подходом:
$$ P(x) = \frac{n(x)}{N} $$где \(n(x)\) — количество раз, когда произошло событие x, а \(N\) — общее количество испытаний.
Для нашего примера с кубиком и событием “выпало четное число”:
$$ P(E) = \frac{n(E)}{N} = \frac{3}{6} = \frac{1}{2} $$где \(n(E)\) — количество раз, когда выпало четное число, а \(N\) — общее количество бросков.
В этой статье мы будем использовать классический подход, так как он проще и интуитивно понятнее. Но итоговые формулы будут одинаковыми для обоих подходов.
Два события: объединение и пересечение
Пусть есть два события E и F. Их пересечение (\(E \cap F\)) — это событие, когда происходят оба события E и F. А объединение (\(E \cup F\)) — это событие, когда происходит хотя бы одно из двух событий E или F.
Например, если E — “выпало четное число”, а F — “выпало число больше 3”, то:
$$ E = \{2, 4, 6\} $$$$ F = \{4, 5, 6\} $$$$ E \cup F = \{2, 4, 5, 6\} $$$$ E \cap F = \{4, 6\} $$Графически это — пересечение двух кругов на диаграмме Венна:
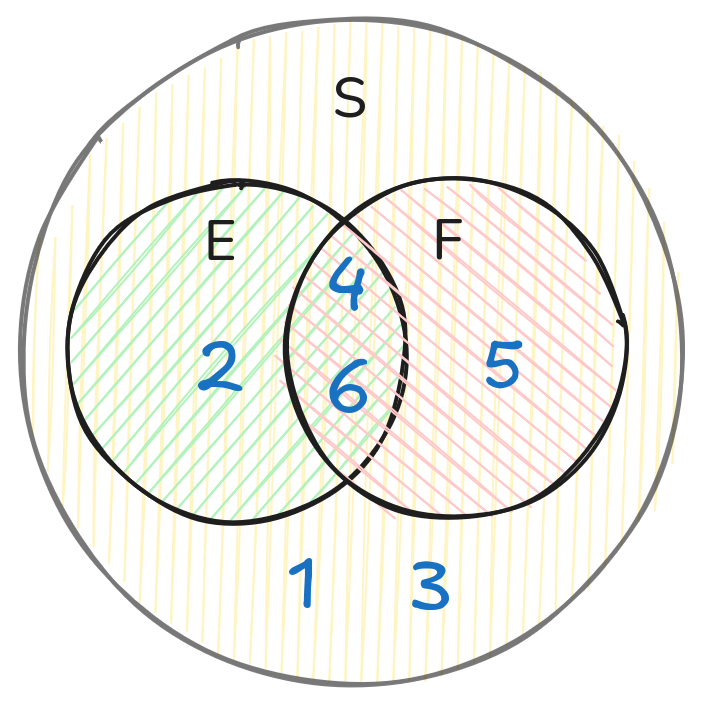
Вероятность того, что произойдет хотя бы одно из двух событий E или F, обозначается \(P(E \cup F)\) и вычисляется по формуле:
$$ P(E \cup F) = \frac{|E|}{|S|} + \frac{|F|}{|S|} - \frac{|E \cap F|}{|S|} = \frac{|E \cup F|}{|S|} = P(E) + P(F) - P(E \cap F) \tag{2} $$Здесь \(P(E \cup F)\) — вероятность того, что произойдет хотя бы одно из двух событий.
Формула учитывает, что если события E и F пересекаются, то элементы пересечения посчитаются дважды, поэтому мы вычитаем \(P(E \cap F)\).
Теперь рассмотрим вероятность пересечения двух событий:
В нашем примере E — “выпало четное число”, а F — “выпало число больше 3”. Тогда:
$$ P(E \cap F) = \frac{|E \cap F|}{|S|} = \frac{|\{4, 6\}|}{|S|} = \frac{2}{6} = \frac{1}{3} $$Зависимость и независимость событий
Теперь рассмотрим зависимость и независимость событий. Если события E и F независимы, то вероятность их пересечения равна произведению вероятностей каждого из них:
$$ P(E \cap F) = \frac{|E \cap F|}{|S|} = \frac{|E|}{|S|} \cdot \frac{|F|}{|S|} = P(E) \cdot P(F) \tag{3} $$Чтобы понять эту формулу интуитивно, представим следующее:
Если \(P(E) = |E|/|S|\) — это доля благоприятных исходов E в пространстве S, а \(P(F) = |F|/|S|\) — доля благоприятных исходов F в пространстве S, то если события независимы, то шанс того, что в части благоприятных исходов E будет еще и часть благоприятных исходов F, будет такой же, как и шанс того, что во всех исходах S будет часть благоприятных исходов F.
А если так, то та часть от S, которая будет в E (\(P(E) \cdot |S|\)), имеет шанс \(P(F)\) содержать благоприятные исходы F. То есть \(P(E) \cdot P(F) = P(E \cap F)\).
Если вероятность события E не зависит от того, произошло ли событие F, то события E и F называются независимыми.
Например, если бросаем кубик дважды, то:
$$ S = \{ (1,1), (1,2), \ldots, (6,6) \} $$Пусть E — “первый бросок — четный”, а F — “второй бросок — четный”. Эти события независимы, так как вероятность четного первого броска не зависит от результата второго броска.
Для каждого броска половина исходов — четные:
$$ P(E) = P(F) = \frac{3}{6} = \frac{1}{2} $$Вероятность того, что оба события произойдут:
$$ P(E \cap F) = P(E) \cdot P(F) $$В нашем примере после первого из всех возможных исходов благоприятных ровно половина, а после второго броска из этой половины тоже половина. То есть:
$$ P(E \cap F) = P(E) \cdot P(F) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} $$Эта формула справедлива только для независимых событий.
Если вероятность события E зависит от того, произошло ли событие F, то события E и F называются зависимыми. Обозначается это как \(P(E|F)\) — вероятность события E при условии, что произошло событие F.
Запомним, что если события E и F независимы, то:
$$P(E|F) = P(E) \tag{4}$$Если же события зависимы, то:
$$P(E|F) \neq P(E)$$
Для понятности рассмотрим два примера:
Пример 1:
Пусть F — “выпало число больше 3”, а E — “выпало четное число”. Тогда:
$$ P(F) = \frac{3}{6} = \frac{1}{2} $$$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Но
$$ P(E|F) = \frac{|E \cap F|}{|F|} = \frac{|\{4, 6\}|}{|\{4, 5, 6\}|} = \frac{2}{3} $$что не равно \(P(E)\).
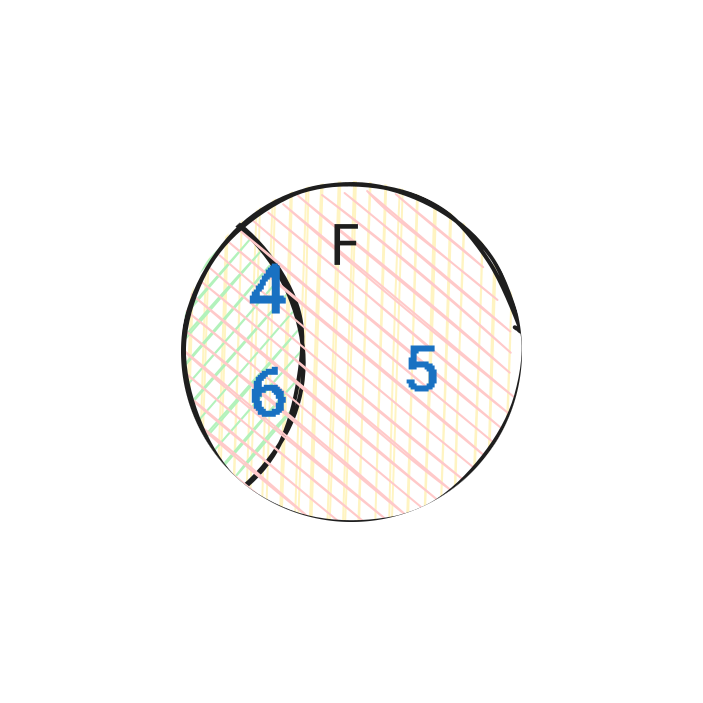
(Из 3 четных чисел {2, 4, 6} два больше 3 — {4, 6})
Если бы события были независимы, то \(P(E|F) = P(E)\). Здесь же \(P(E|F) > P(E)\), значит события зависимы.
Пример 2:
Пусть E — «выпало одно из чисел {1,2,3}», а F — «выпало одно из чисел {1,2,4,6}».
Если произошло событие F, то для наступления события E (выпало одно из {1,2,3}) нужно, чтобы выпало 1 или 2. Проверим это математически:
$$ P(F) = \frac{4}{6} = \frac{2}{3} $$$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Теперь найдём \(P(E|F)\):
$$ P(E|F) = \frac{|E \cap F|}{|F|} = \frac{2}{4} = \frac{1}{2} $$Обратите внимание: так как известно, что произошло событие F (выпало одно из {1,2,4,6}), мы рассматриваем только эти числа. В числителе — \(E \cap F\), в знаменателе — количество элементов в F.
Сравним \(P(E|F)\) и \(P(E)\): они равны, значит события независимы.
Если нам сообщили: «Выпало число из F (то есть 1, 2, 4 или 6)», это не меняет вероятность попадания в E (без знания F: {1,2,3} из {1,2,3,4,5,6}; зная F: {1,2} из {1,2,4,6}). Она остаётся 3/6 = 2/4 = 0.5. Значит, информация о F не помогает понять, случилось ли E.
Независимость — это информационная слепота:
Знание одного события не даёт информации о втором.
Как же быть, если события зависимы? Чему равна вероятность события E при условии, что произошло событие F?
Аналогично тому, как мы объясняли формулу пересечения вероятности независимых событий, мы можем рассуждать и о зависимых событиях.
Если событие F произошло, то мы можем рассматривать только те исходы, которые соответствуют событию F. В случае зависимых событий, доля благоприятных исходов Е которые пересекаются с F уже не равна доле всех благоприятных исходов E в пространстве S.
А если так, когда произошло F - шанс того что случится и E поменялся! Мы можем записать формулу для условной вероятности события E при условии, что произошло событие F:
$$ P(E \cap F) = P(E|F) \cdot P(F) \tag{5} $$Отсюда следует, что:
$$ P(E|F) = \frac{P(E \cap F)}{P(F)} \tag{6} $$Так как пересечение двух событий E и F — это событие, которое произошло одновременно, мы можем аналогично выразить вероятность P(E∩F) через условную вероятность события F при условии, что произошло событие E:
$$ P(E \cap F) = P(F|E) \cdot P(E) \tag{7} $$Приравняв правые части (5) и (7), получаем:
$$ P(E|F) \cdot P(F) = P(F|E) \cdot P(E) $$или
$$ P(E|F) = \frac{P(F|E) \cdot P(E)}{P(F)} \tag{8} $$ЭТО И ЕСТЬ ТЕОРЕМА БАЙЕСА!
Это формула, которая связывает условные вероятности двух событий E и F. Она позволяет вычислить вероятность события E при условии, что произошло событие F, зная вероятность события F при условии, что произошло событие E.
Часто P(F) неизвестна, но можно выразить её через полную вероятность события F:
Формула полной вероятности:
$$ P(F) = P(F|E) \cdot P(E) + P(F| \neg E) \cdot P(\neg E) \tag{9} $$где \(\neg E\) — это событие, противоположное событию E.
Байесовская теорема — это формула, которая связывает условные вероятности двух событий E и F. Она позволяет вычислить вероятность события E при условии, что произошло событие F, зная вероятность события F при условии, что произошло событие E.
Это очень полезная формула, которая позволяет вычислять вероятности событий, когда известны другие вероятности. Она широко используется в статистике, машинном обучении и других областях.
Каждый из этих элементов формулы имеет своё значение:
- P(E|F) — апостериорная вероятность (то, что мы хотим узнать)
- P(E) — априорная вероятность (начальное предположение)
- P(F|E) — правдоподобие (likelihood)
- P(F) — полная вероятность события F
Детально рассмотрение каждого их этих элементов выходит за рамки этой статьи, но в целом можно сказать, что:
- A priori (априорная) вероятность — это вероятность события до получения новой информации.
- A posteriori (апостериорная) вероятность — это вероятность события после получения новой информации.
- Правдоподобие (likelihood) — это вероятность наблюдать данные, если гипотеза верна.
- Полная вероятность (marginal likelihood) — это вероятность наблюдать данные, независимо от гипотезы.
Каждая из этих вероятностей имеет своё значение и используется в качестве основ для алгоритмов статистики и машинного обучения, таких как байесовские сети, наивный байесовский классификатор, MLE, ELBO, MCMC и многие другие.
Дед Иван, условная вероятность и теорема Байеса
Условная вероятность
Рассмотрим пример.
Дед Иван попал на пивной фестиваль. Организаторы устроили розыгрыш: из 50 бутылок (40 светлых, из которых 9 безалкогольных, и 10 темных, из которых 3 безалкогольных).

Пример 1:
Начнём с простого вопроса: “Какова вероятность того, что бутылка безалкогольная?” Ответ прост: 12/50 = 0.24.
Но что, если мы знаем, что бутылка темная? Какова вероятность того, что она безалкогольная?
В этом случае мы рассматриваем только темные бутылки. Из 10 темных бутылок 3 безалкогольные, значит вероятность 3/10 = 0.3.
Теперь с помощью формулы Байеса мы можем выразить вероятность того, что бутылка темная, при условии, что она безалкогольная:
$$ P(\text{темная} | \text{безалкогольная}) = \frac{P(\text{безалкогольная} | \text{темная}) \cdot P(\text{темная})}{P(\text{безалкогольная})} = \frac{3/10 \cdot 10/50}{12/50} = \frac{3}{12} = 0.25 $$Это совпадает с интуитивным пониманием: из 12 безалкогольных бутылок 3 темные, значит вероятность того, что безалкогольная бутылка темная, равна 0.25.
Пример 2:
Дед Иван и его друг Петрович соревнуются, кто лучше определяет пиво.
- Оба независимо пробуют одну и ту же бутылку. Дед Иван правильно определяет тип пива с вероятностью 0.7, а Петрович – с вероятностью 0.65. Какова вероятность, что хотя бы один из них правильно определит тип случайно выбранного пива?
Решение:
$$ P(\text{хотя бы один}) = 1 - P(\text{оба ошиблись}) = 1 - P(\text{ошибка дед Ивана}) \cdot P(\text{ошибка Петровича}) = $$$$ = 1 - (1 - 0.7) \cdot (1 - 0.65) = 1 - 0.3 \cdot 0.35 = 1 - 0.105 = 0.895 $$- Дед Иван с завязанными глазами попробовал пиво и сказал, что оно темное алкогольное. Известно, что он правильно определяет светлое алкогольное с вероятностью 0.7, светлое безалкогольное с вероятностью 0.6, темное алкогольное с вероятностью 0.8 и темное безалкогольное с вероятностью 0.7. Если дед Иван заявляет, что пиво светлое, какова вероятность, что оно алкогольное?
Решение:
Количество бутылок разных типов:
- Светлое алкогольное: 40 - 9 = 31 бутылка
- Светлое безалкогольное: 9 бутылок
- Темное алкогольное: 10 - 3 = 7 бутылок
- Темное безалкогольное: 3 бутылки
Вероятности различных типов пива:
$$P(\text{светлое алкогольное}) = \frac{31}{50} = 0.62$$Определим вероятности определения “светлое” для каждого типа пива:
- Если пиво светлое алкогольное: $$P(\text{скажет "светлое"} | \text{светлое алкогольное}) = 0.7$$
- Если пиво светлое безалкогольное: $$P(\text{скажет "светлое"} | \text{светлое безалкогольное}) = 0.6$$
- Если пиво темное алкогольное: $$P(\text{скажет "светлое"} | \text{темное алкогольное}) = 1 - 0.8 = 0.2$$
- Если пиво темное безалкогольное: $$P(\text{скажет "светлое"} | \text{темное безалкогольное}) = 1 - 0.7 = 0.3$$
По формуле полной вероятности:
$$P(\text{скажет "светлое"}) = \sum_i P(\text{скажет "светлое"} | \text{тип}_i) \cdot P(\text{тип}_i)$$$$P(\text{скажет "светлое"}) = 0.7 \cdot 0.62 + 0.6 \cdot 0.18 + 0.2 \cdot 0.14 + 0.3 \cdot 0.06$$Найдем вероятность алкогольного пива:
Теперь используем формулу Байеса (8). Сначала найдем вероятность того, что дед Иван скажет “светлое” при условии, что пиво алкогольное:
$$P(\text{скажет "светлое"} | \text{алкогольное}) = \frac{P(\text{скажет "светлое"} | \text{светлое алк}) \cdot P(\text{светлое алк}) + P(\text{скажет "светлое"} | \text{темное алк}) \cdot P(\text{темное алк})}{P(\text{алкогольное})}$$$$P(\text{скажет "светлое"} | \text{алкогольное}) = \frac{0.7 \cdot 0.62 + 0.2 \cdot 0.14}{0.76} = \frac{0.434 + 0.028}{0.76} = \frac{0.462}{0.76} = 0.6079$$Наконец, применяем формулу Байеса:
$$P(\text{алкогольное} | \text{скажет "светлое"}) = \frac{P(\text{скажет "светлое"} | \text{алкогольное}) \cdot P(\text{алкогольное})}{P(\text{скажет "светлое"})} = \frac{0.6079 \cdot 0.76}{0.588} = \frac{0.462}{0.588} \approx 0.7857$$Таким образом, если дед Иван сказал, что пиво светлое, то вероятность того, что оно алкогольное, составляет примерно 78.57%.