Введение
Работы Фрэнка Розенблатта (Frank Rosenblatt) положили основу сегодняшних нейронных сетей. Он заложил принципы, которые и по сей день остаются актуальными, а также заложил фундамент для дальнейших исследований в области машинного обучения. В этой статье я представлю основные идеи, которые он предложил, и попробую провести параллели с современными нейронными сетями. Я также покажу, как реализовать перцептрон на Python с использованием библиотеки NumPy.
Что такое нейрон?
Наш мозг состоит из миллиардов клеток, которые называются нейронами. Нейрон — это основная единица нервной системы, которая отвечает за передачу и обработку информации.
Нейро́н или нервная клетка (от др.-греч. νεῦρον «волокно; нерв») — узкоспециализированная клетка. Нейрон — электрически возбудимая клетка, которая предназначена для приёма извне, обработки, хранения, передачи и вывода вовне информации с помощью электрических и химических сигналов. (Wikipedia)
Каждый нейрон получает сигналы от других нейронов и передает их дальше. Нейроны связаны между собой синапсами, которые позволяют им обмениваться информацией.
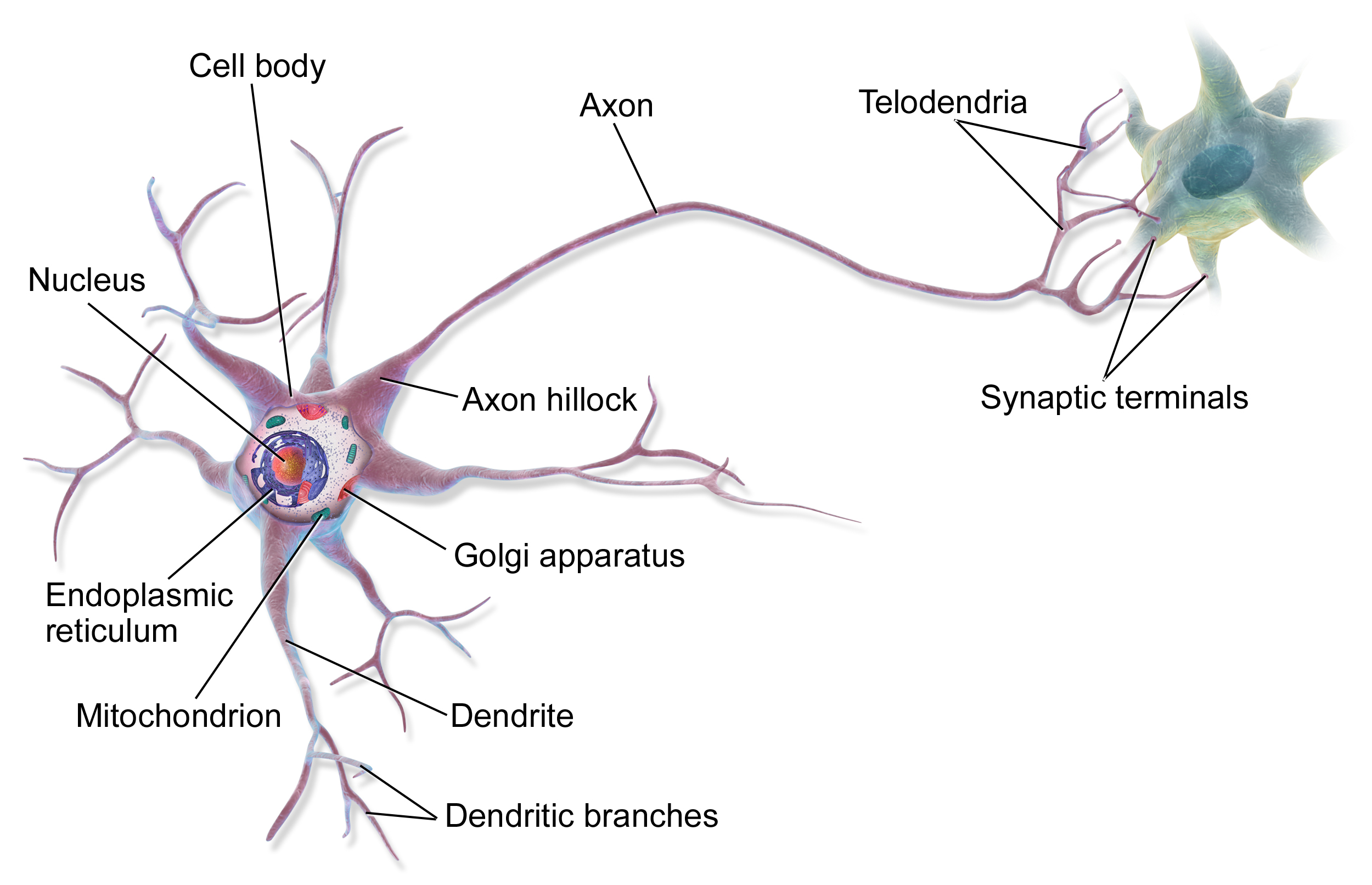
Обратим внимание на дендриты и аксон. Дендриты принимают сигналы от других нейронов, а аксон передает сигналы дальше. Каждый нейрон может иметь множество дендритов и один аксон (в большинстве случаев). Сигналы, которые нейрон получает от других нейронов, могут быть как возбуждающими, так и тормозящими. Возбуждающие сигналы увеличивают вероятность того, что нейрон “сработает” (т.е. передаст сигнал дальше), а тормозящие — уменьшают эту вероятность.
Итак в 1957 году Фрэнк Розенблатт предложил модель нейрона, которую он и назвал перцептроном.
Что такое перцептрон?
Перцептрон — это простейшая модель нейронной сети, которая состоит из одного нейрона. Он принимает на вход несколько сигналов (входов), обрабатывает их и выдает один сигнал (выход).
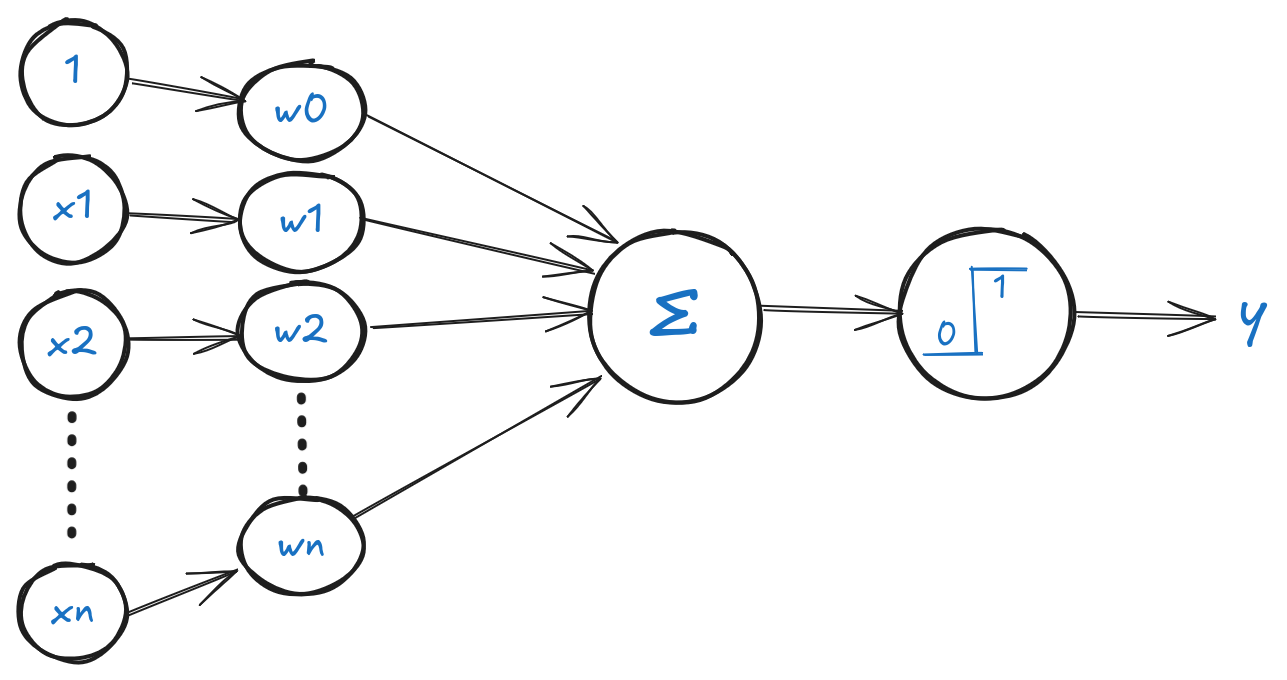
В своей модели Розенблатт использовал несколько входов, каждый из которых имел свой вес. Вес — это число, которое показывает, насколько важен этот вход для нейрона. Чем больше вес, тем больше влияние этого входа на выход нейрона.
Входы и веса перемножаются, и затем все произведения суммируются. Если сумма больше порога, то нейрон “срабатывает” и выдает сигнал 1, иначе — 0. Порог — это число, которое показывает, насколько сильным должен быть сигнал, чтобы нейрон “сработал”. Порог можно считать весом, который умножается на 1 (вход всегда равен 1).
В современных нейронных сетях порог обычно заменяется на функцию активации, которая позволяет нейрону “срабатывать” при определенных условиях. Функция активации может быть линейной или нелинейной. В линейной функции активации выход нейрона пропорционален входу, а в нелинейной — выход зависит от входа по сложной формуле.
Давайте запишем формулу перцептрона:
Если на входе у нас есть вектор \(x = (x_1, x_2, \ldots, x_n)\), а на выходе — число \(y\). Тогда формула перцептрона выглядит так:
Сумма всех входов умноженных на веса:
где i - номер примера, \(\theta\) - вектор весов, \(x^{(i)}\) - вектор входов.
Тогда функция активации (шаговая функция):
$$ h(z)= \left\{ \begin{array}{rcr} 1 & z \geq 0 \\ 0 & иначе \\ \end{array} \right. \tag2 $$Давайте напишем код, который реализует перцептрон. Мы будем использовать библиотеку NumPy для работы с массивами и матрицами. Также мы будем использовать библиотеку Matplotlib для визуализации данных.
import numpy as np
class Perceptron:
def __init__(self):
pass
def net_input(self,X):
return np.dot(X, self.theta[1:]) + self.theta[0] # z
def predict(self,X):
return np.where(self.net_input(X) >= 0.0, 1, 0) # h(z)
Вы наверняка заметили в коде, что мы добавили единицу к весам. Это делается для того, чтобы учесть порог. Мы можем считать, что у нас есть дополнительный вход, который всегда равен 1. Этот вход умножается на вес, который равен порогу. Таким образом, мы можем считать, что порог — это вес, который умножается на 1.
Также изначальные веса нам неизвестны, поэтому мы инициализируем их нулями. И перед нами стоит задача найти такие веса, которые позволят перцептрону правильно классифицировать данные.
Как обучить перцептрон?
Перед тем как обучить перцептрон, давайте определим, что такое обучение. Обучение — это процесс, в котором мы находим такие веса, которые позволят перцептрону правильно классифицировать данные. То есть у нас есть входные данные x₁…xₙ и выходные данные y (0 или 1), и мы хотим найти такие веса \(\theta\), которые позволят перцептрону правильно классифицировать данные.
Для этого нам нужно определить функцию потерь. Функция потерь — это функция, которая показывает, насколько хорошо перцептрон классифицирует данные. Чем меньше значение функции потерь, тем лучше перцептрон классифицирует данные (тем меньше потери - отсюда и название).
$$ error^{(i)} = \frac12(h(z^{(i)}) - y^{(i)})^2 \tag3$$Давайте разберемся почему в этой формуле квадрат. Если бы мы использовали просто разность, то при обучении перцептрон мог бы “путаться” в знаках.
Тогда общая функция потерь будет равна:
$$ L(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h(z^{(i)}) - y^{(i)})^2 \tag4 $$Мы делим результат на m, чтобы получить среднее значение потерь. m — это количество примеров в обучающей выборке.
Если мы предсказываем 1, а на самом деле 0, то ошибка будет равна (1-0) = 1, а если наоборот, то ошибка будет равна (0-1) = -1. Если бы мы использовали просто разность, то в первом случае ошибка была бы положительной, а во втором — отрицательной. И при суммировании ошибки бы взаимно уничтожались. Если мы возьмем квадрат, то в обоих случаях ошибка будет положительной. Таким образом, мы можем считать, что ошибка — это расстояние от предсказания до реального значения. Чем меньше это расстояние, тем лучше перцептрон классифицирует данные.
Так как данные - фиксированы, то мы можем считать их константами. Тогда функция потерь будет зависеть только от весов \(\theta\). То есть мы можем считать, что функция потерь — это функция от весов.
Так как наша функция потерь является квадратичной, то её производная будет линейной и равняться 0 в точке минимума. Для упрощения вычисления производной умножим функцию потерь на 1/2 (это не повлияет на минимум, так как 1/2 - это просто константа). Тогда производная для примера i будет равна:
$$ \frac{\partial{\frac12(\theta_0+\theta_1x_1^{(i)} + \theta_2x_2^{(i)} + ... + \theta_nx_n^{(i)} - y^{(i)} )^2}}{\partial{\theta_j}} = (h(z^{(i)}) - y^{(i)})x_j^{(i)} $$и общая производная по правилу суммы будет равна:
$$ \frac{\partial{L(\theta)}}{\partial{\theta_j}} = \frac{1}{m} \sum_{i=1}^{m} (h(z^{(i)}) - y^{(i)})x_j^{(i)} \tag5 $$для j = 0, 1, …, n
Чтобы решить задачу аналитически, нам бы пришлось приравнять каждую частную производную к нулю и решить уравнение. Но это как правило невозможно сделать. если у нас 100 примеров по 100 признаков в каждом (m = 100 и x₁…x₁₀₀), нам бы пришлось решить систему из 100 уравнений со 100 неизвестными. Поэтому мы будем использовать численные методы для нахождения минимума функции потерь. Один из самых простых и популярных методов — это метод градиентного спуска.
Градиентный спуск
Градиентный спуск — это итеративный метод, который позволяет находить минимум функции.
Идея этого метода в том, что если мы изменим вес \(\theta_j\) на небольшое значение, то функция потерь (3) изменится приблизительно на:
$$ \Delta{error} =(h(z^{(i)}) - y^{(i)})x_j^{(i)}\Delta{\theta_j} $$Так, для того чтобы уменьшить ошибку, нам нужно изменить вес \(\theta_j\) в сторону, противоположную производной (так как производная показывает направление, в котором функция растет). То есть мы должны уменьшить вес, если производная положительная, и увеличить вес, если производная отрицательная. Мы можем записать это в виде формулы:
$$ \Delta{\theta_j} = \alpha = learningrate(шаг\ обучения) $$$$ \theta_j = \theta_j - \alpha(h(z^{(i)}) - y^{(i)}) x_j^{(i)} \tag6 $$Шаг обучения не должен быть слишком большим, иначе мы можем “перепрыгнуть” минимум и начать двигаться в другую сторону. Если шаг обучения слишком маленький, то процесс обучения будет слишком долгим. Поэтому нужно подбирать его экспериментально.
Реализация
Давайте сами напишем функцию, которая будет обучать перцептрон. Но сначала определимся с данными.
Один из наиболее популярных наборов данных для обучения перцептрона — это набор данных Ирисов (Iris dataset). Он состоит из 150 примеров, каждый из которых имеет 4 признака (длина и ширина чашелистика и лепестка) и 3 класса (виды ирисов). Мы будем использовать только два класса (Setosa и Versicolor), чтобы упростить задачу (Wikipedia).
Установим необходимые библиотеки и загрузим данные:
pip install numpy matplotlib pandas
Теперь запустим Jupyter Notebook и загрузим данные:
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
header=None)
df.tail()
Вывод:
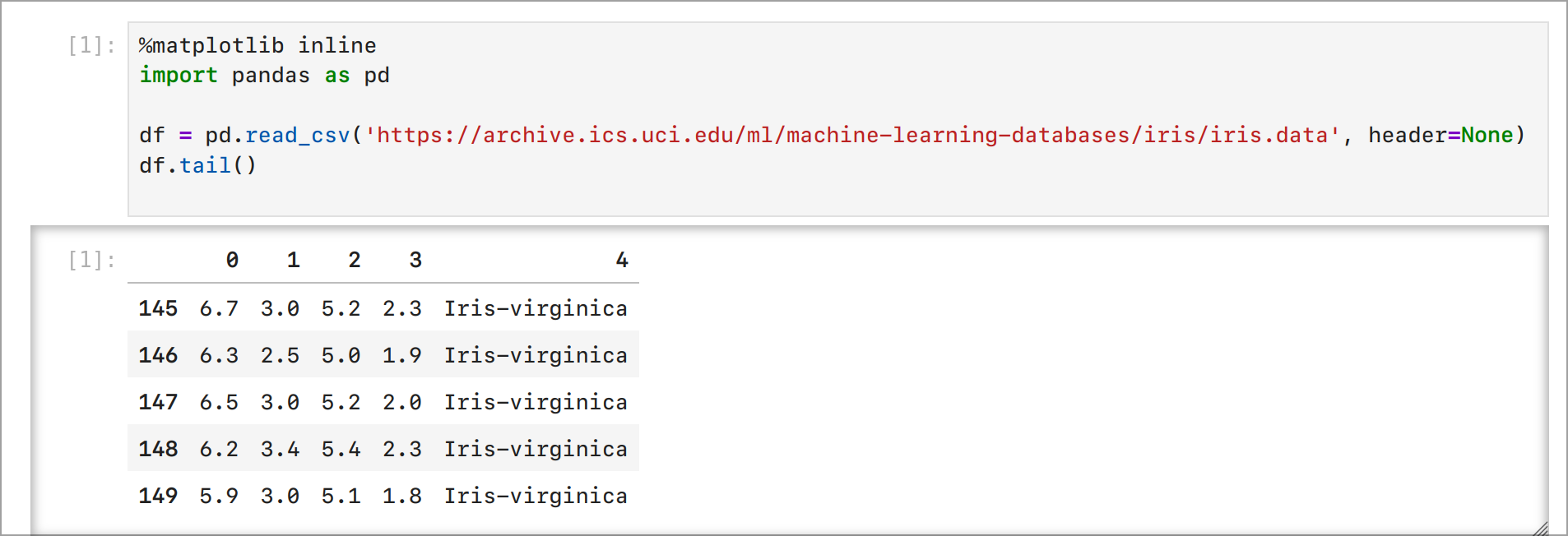
Давайте отобразим данные:
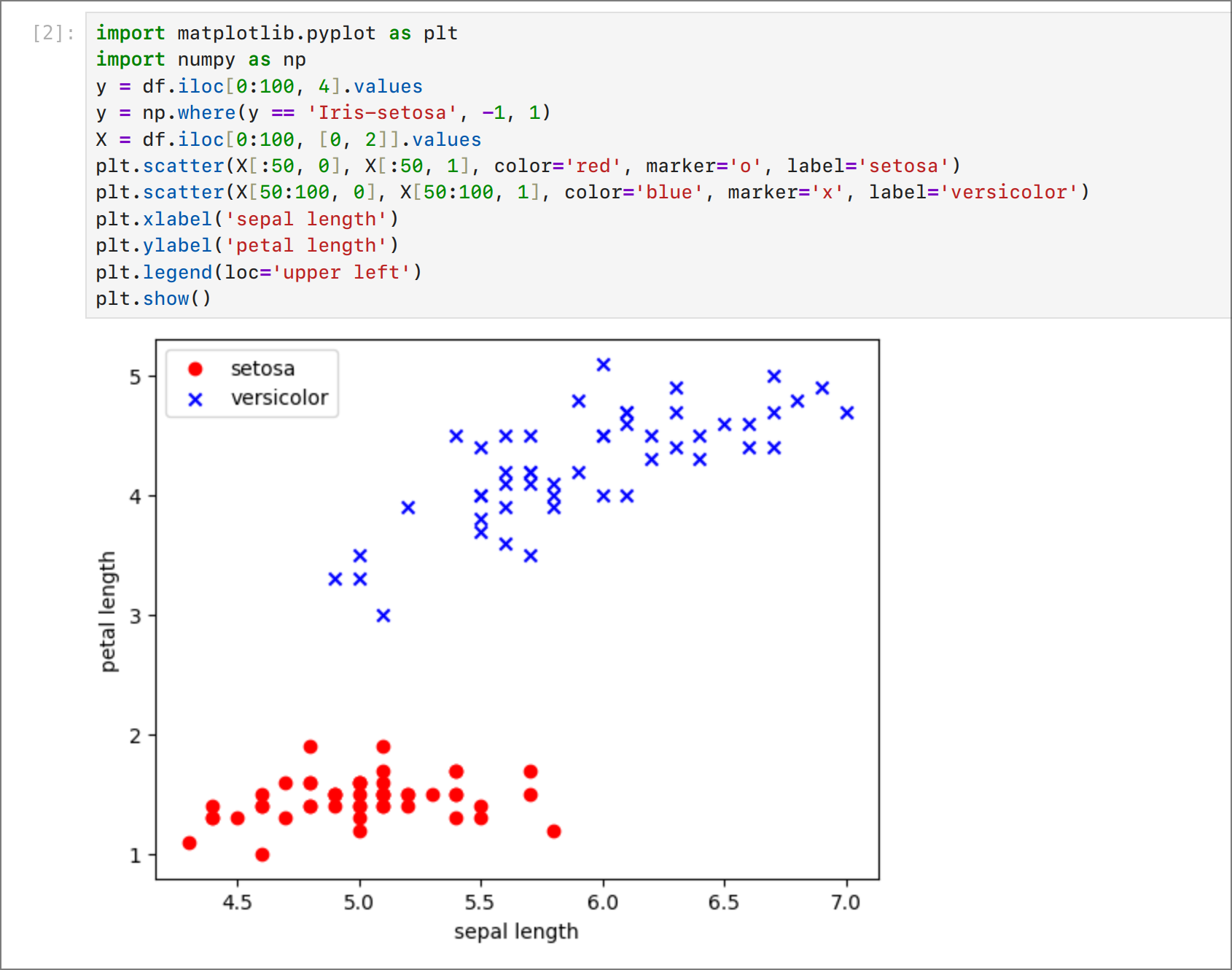
Мы можем заметить, что данные линейно разделимы. То есть мы можем провести прямую линию, которая разделит данные на два класса. Это значит, что мы можем использовать перцептрон для решения этой задачи. Если бы данные были не линейно разделимы, то нам бы пришлось использовать более сложные модели (например, многослойные нейронные сети).
Обновим код, чтобы он включал в себя обучение перцептрона (fit метод) и массив с ошибками для отслеживания процесса обучения:
import numpy as np
class Perceptron:
def __init__(self,alpha=0.01, n_iter=10):
self.alpha = alpha
self.n_iter = n_iter
self.wrong_classifications = []
def fit(self, X, y):
self.theta = np.zeros(X.shape[1] + 1) # веса
for _ in range(self.n_iter):
wrong_classification = 0
for xi, target in zip(X, y):
update = self.alpha * (target - self.predict(xi))
self.theta[1:] += update * xi
self.theta[0] += update
wrong_classification += int(update != 0.0)
self.wrong_classifications.append(wrong_classification)
return self
def net_input(self,X):
return np.dot(X, self.theta[1:]) + self.theta[0] # z
def predict(self,X):
return np.where(self.net_input(X) >= 0.0, 1, 0) # h(z)
Теперь вызовем метод fit и передадим ему данные:
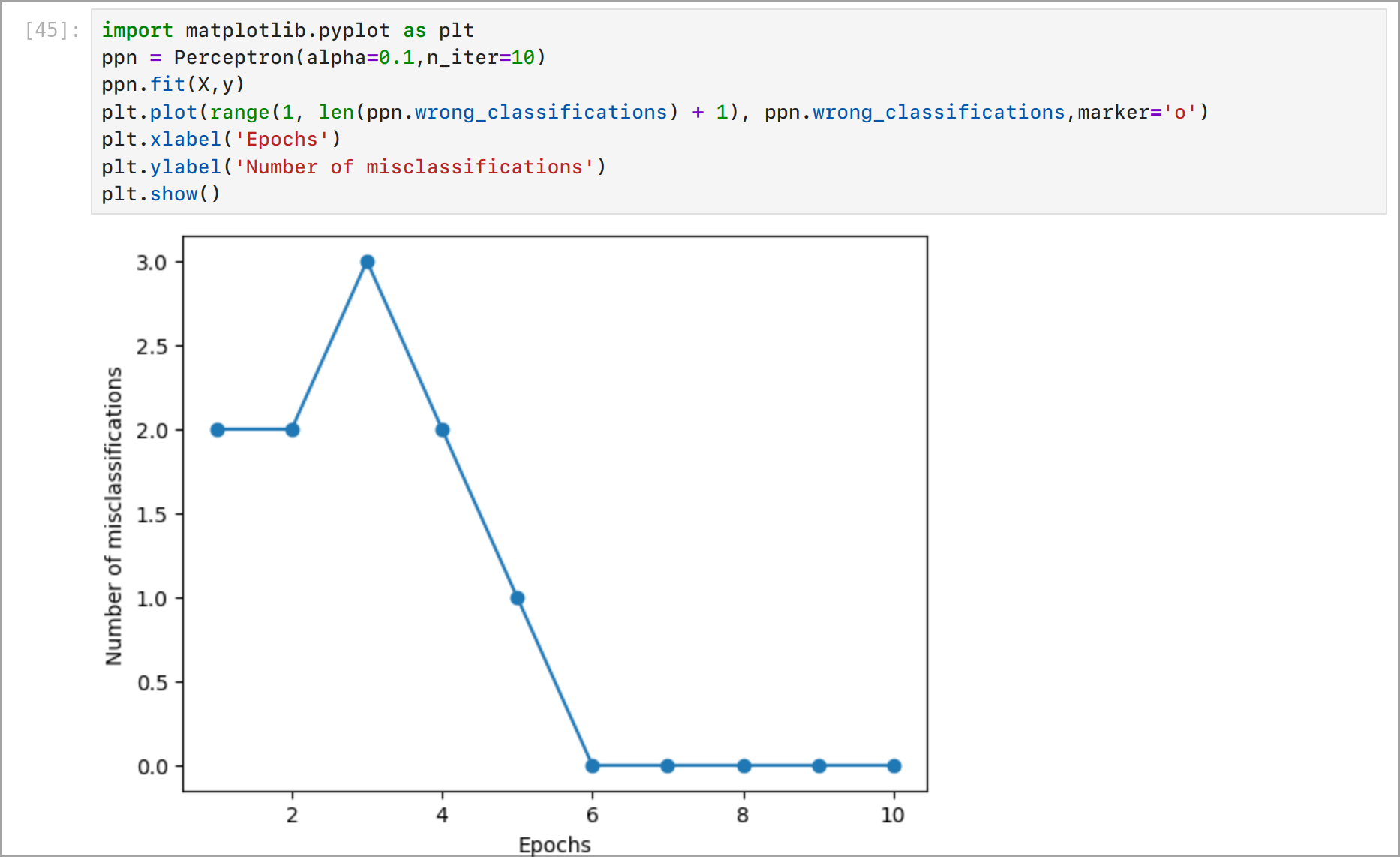
Как видите, спустя 6 шагов перцептрон научился классифицировать данные. Теперь давайте посмотрим на границу принятия решения. Мы можем визуализировать границу принятия решения, используя библиотеку Matplotlib.
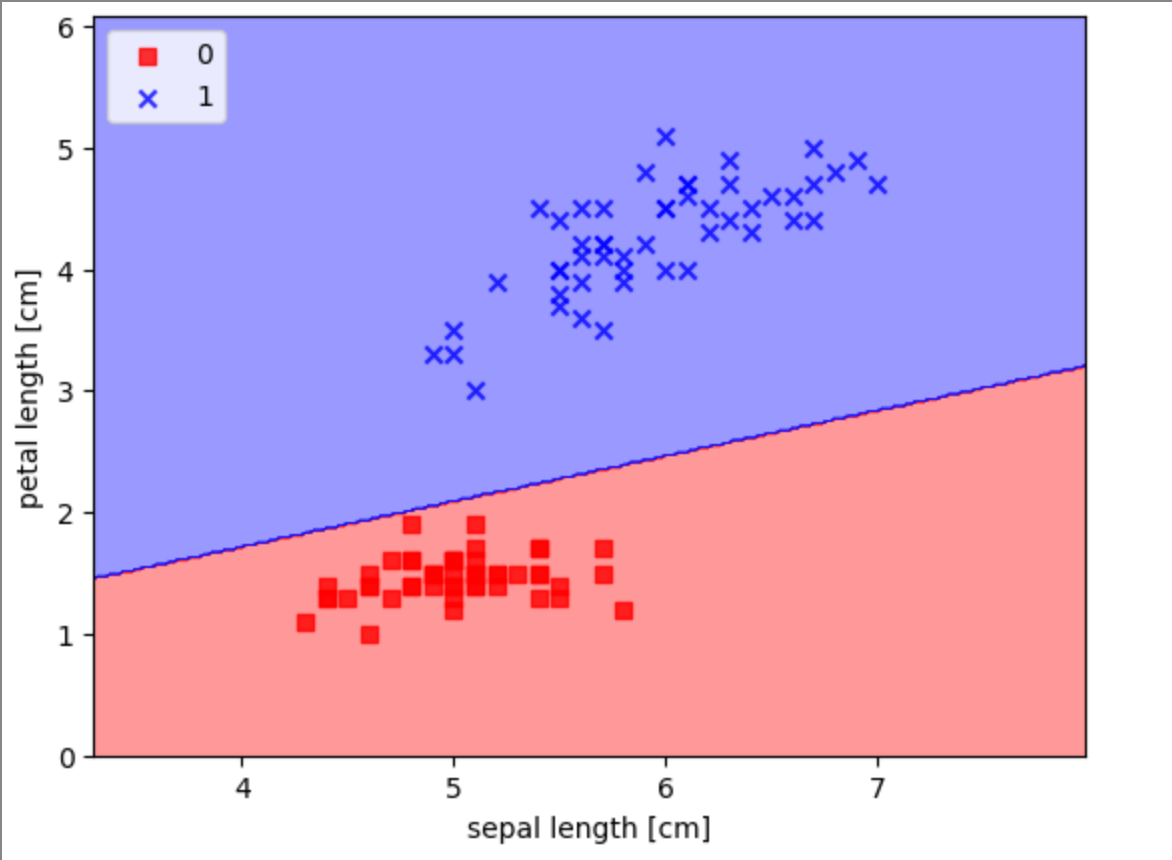
Заключение
В этой статье мы рассмотрели перцептрон — простейшую модель нейронной сети. Мы узнали, как он работает и как его обучить. Мы также рассмотрели метод градиентного спуска, который позволяет находить минимум функции потерь. Надеюсь, что эта статья была полезна для вас и помогла вам лучше понять, как работают нейронные сети.